This is a little script will generate a joint probability tree that you can view and download. My hope is that this will be a useful tool for pedagogical purposes or just some good, old-fashioned fun with statistics. This is not a general-purpose decision tree generator, because it has the following constraints:
- All events are mutually exclusive.
- Each iteration of the tree represents sampling without replacement.
- All events are collectively exhaustive.
If you are not familiar with any of the 3 bolded terms above, please click on each term to read its definition in Wikipedia.
To generate a probability tree, enter the parameters of your tree in the input boxes below. On the next page, you will be asked to provide information about each of your mutually exclusive events, specifically to provide a label for each event and the initial probability of obtaining it. On the third page, you will see your tree displayed as a PNG image in your web browser that can be downloaded for future use! An example probability tree and the input that generated is displayed below.
Important Notes: Currently, there are two unfortunate-but-necessary constraints on this Joint Probability Tree Generator:
- The first constraint is the tree generator takes probabilities in fractional units (the denominator of which will be the same for all your probabilities). If you want to evaluate a joint probability tree where probabilities are represented as decimals (e.g., P(A) = .7, P(A') = .3), then please enter a value of 10n for your denominator below (i.e., P(A) = .7 = 7/10, P(A') = .3 = 3/10).
- The second constraint is that, due to bandwidth issues, the size of the probability trees that can be generated are restricted based on number of events and number of iterations to the tree. If you have 2 mutually exclusive events, you can generate a probability tree with up to 8 iterations. If you have 3 mutually exclusive events, then you can only generate trees with up to 5 iterations. Trees with 4 mutually exclusive events are capped at 4 iterations; trees with 5 - 7 mutually exclusive events is capped at 3 iterations; trees with between 8 - 21 mutually exclusive events are capped at 2 iterations. I cannot generate trees with more than 21 mutually exclusive events.
Sorry. I expect to expand these capabilities in the near future.
Here is a joint probability tree that was generated to evaluate the likelihood of getting blackjack (an Ace plus a card that is worth 10) in two draws from a well shuffled deck of cards. Below the example tree, I provide the input that was given to the Joint Probability Tree Generator to generate this tree, and explain how it can be used to calculate the probability of obtaining blackjack in two draws from a standard deck of cards.
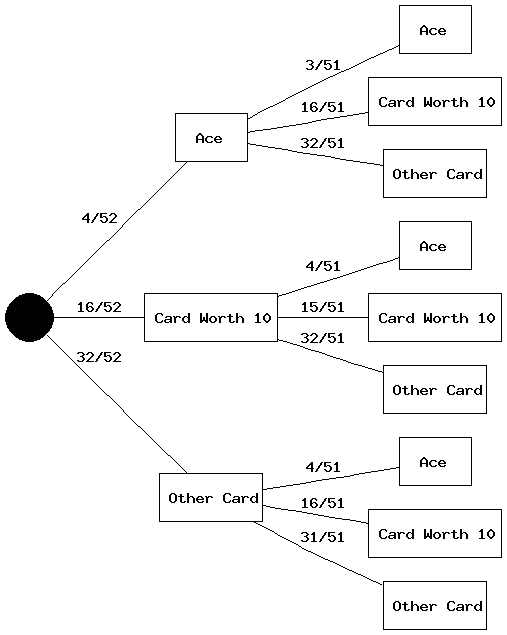
To generate this tree, the following input was submitted to this Joint Probability Tree Generator:
- Events: 3 (One event is getting an Ace, the second is getting a card worth 10, and the third is getting any other card)
- Iterations: 2 (I generated this tree to represent drawing 2 cards in a standard deck)
- Total Possible Outcomes: 52 (This represents a standard deck of 52 cards)
- Event 1: Drawing an Ace
- Event 1 Label: Ace
- Event 1 Initial Likelihood: 4 (There are 4 Aces in a standard deck of cards)
- Event 2: Drawing a King, Queen, Jack, or 10
- Event 2 Label: Card Worth 10
- Event 2 Initial Likelihood: 16 (There are 4 types of cards that are worth 10 in blackjack -- King, Queen, Jack, and 10 -- and there are 4 of each card in a standard deck: 4 x 4 = 16)
- Event 3: Drawing any Other Card
- Event 3 Label: Other Card
- Event 3 Initial Likelihood: 32 (There are 8 cards that are worth less than 10 in blackjack -- 2, 3, 4, 5, 6, 7, 8, and 9 -- and there are 4 of each card in a standard deck: 8 x 4 = 32)
After this tree has been generated, I can use the paths to determine the likelihood of obtaining blackjack in two draws. In this case, there are two ways I could get blackjack, either by drawing an Ace first and a card worth 10 second, or vice versa. To calculate the probability of getting black jack, I would multiply the probabilities along each path that gives me blackjack to get a joint probability for that path, and then add all the successful paths together to get my total probability of obtaining blackjack in two draws. So:
- Blackjack Path 1 - Ace on first draw, Card Worth 10 on second draw: (4/52) x (16/51) = 64/2652 = 16/663
- Blackjack Path 2 - Card Worth 10 on first draw, Ace on second draw: (16/52) x (4/51) = 64/2652 = 16/663
- Probability of Obtaining Black Jack in Two Draws: (16/663) + (16/663) = 32/663 ≈ .0483